[14] Finite Camera Matrix

본 포스트는 학습한 것을 정리할 목적으로 작성되었습니다.

 

해당 포스트의 내용 및 그림, 수식 등은 'Multiple View Geometry in Computer Vision' 책을 참고하였습니다. 

 

 

(1) The basic pinhole model

 

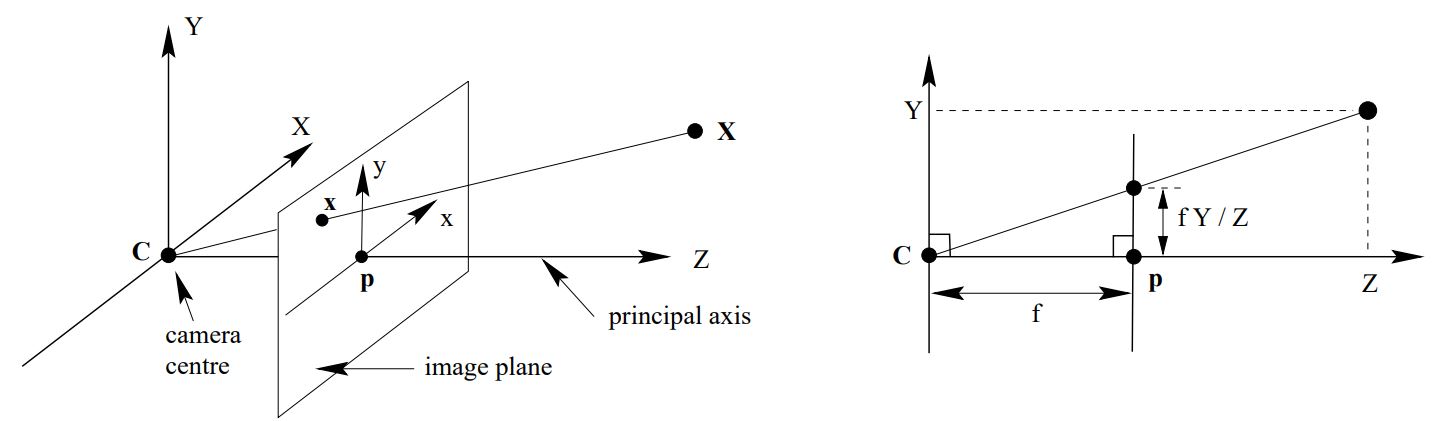
Pinhole camera geometry

여기에서는 공간 내의 점들의 평먼 상의로의 central projection을 다룬다. Projection의 중심을 Euclidean coodrinate system의 origin으로 두고 image plane(focal plane)을 $z=f$라고 한다면 공간상의 점 $\textbf{X}=[X \ Y \ Z]^T$는 다음과 같이 image plane으로 mapping된다.

 

$$ \begin{bmatrix} X & Y & Z \end{bmatrix}^T \ \longmapsto \ \begin{bmatrix} fX/Z & fY/Z \end{bmatrix}^T $$

 

(2) Central projection using homogeneous coordinates

 

이를 homogeneous coordinates를 사용하여 matrix 형태로 표현하면 아래와 같다.

 

$$ \begin{bmatrix} fX \\ fY \\ Z \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} $$

 

$$ \textbf{x} = P\textbf{X}$$

 

$$ P=diag(f, f, 1)[I | \textbf{0}] $$

 

(3) Pirincipal point offset

 

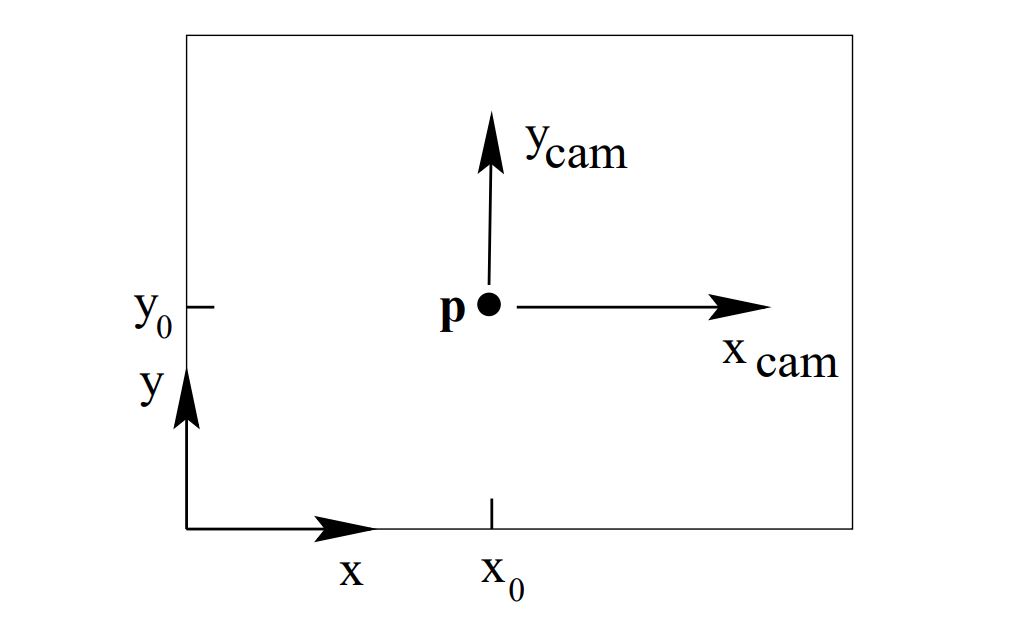
Image $(x,\ y)$ and camera $(x_{cam}, \ y_{cam})$ coordinate systems

(2)의 수식은 image plane의 origin이 principal point에 있음을 가정하였다. 여기에서는 좀 더 일반적으로 이 둘이 다르다고 가정하고 위 그림에서와 같이 image plane 상의 principal point의 좌표를 설정하고 다음과 같이 projection 수식을 전개한다.

 

$$ \begin{bmatrix} X & Y & Z \end{bmatrix}^T \ \longmapsto \ \begin{bmatrix} fX/Z +p_x & fY/Z  + p_y \end{bmatrix}^T $$

 

$$ \begin{bmatrix} fX +Zp_x \\ fY +Zp_y \\ Z \end{bmatrix} = \begin{bmatrix} f & 0 & p_x & 0 \\ 0 & f & p_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} $$

 

이 때 $K=\begin{bmatrix} f & 0 & p_x \\ 0 & f & p_y \\ 0 & 0 &1 \end{bmatrix}$를 $camera \ calibration \ matrix$라고 하고 이를 통해 다음과 같이 표현할 수 있다.

 

$$ \textbf{x} = K[I|\textbf{0}]\textbf{X}_{cam} $$

 

위 식에서 $\begin{bmatrix} X & Y & Z & 1 \end{bmatrix}^T = \textbf{X}_{cam}$이라고 표현하였다. 이는 camera의 center가 Euclidean coordinate system의 origin에 있고 principal axis와 Z축이 같다는 가정 하에 성립한다.

 

(4) Camera rotation and translation

 

 

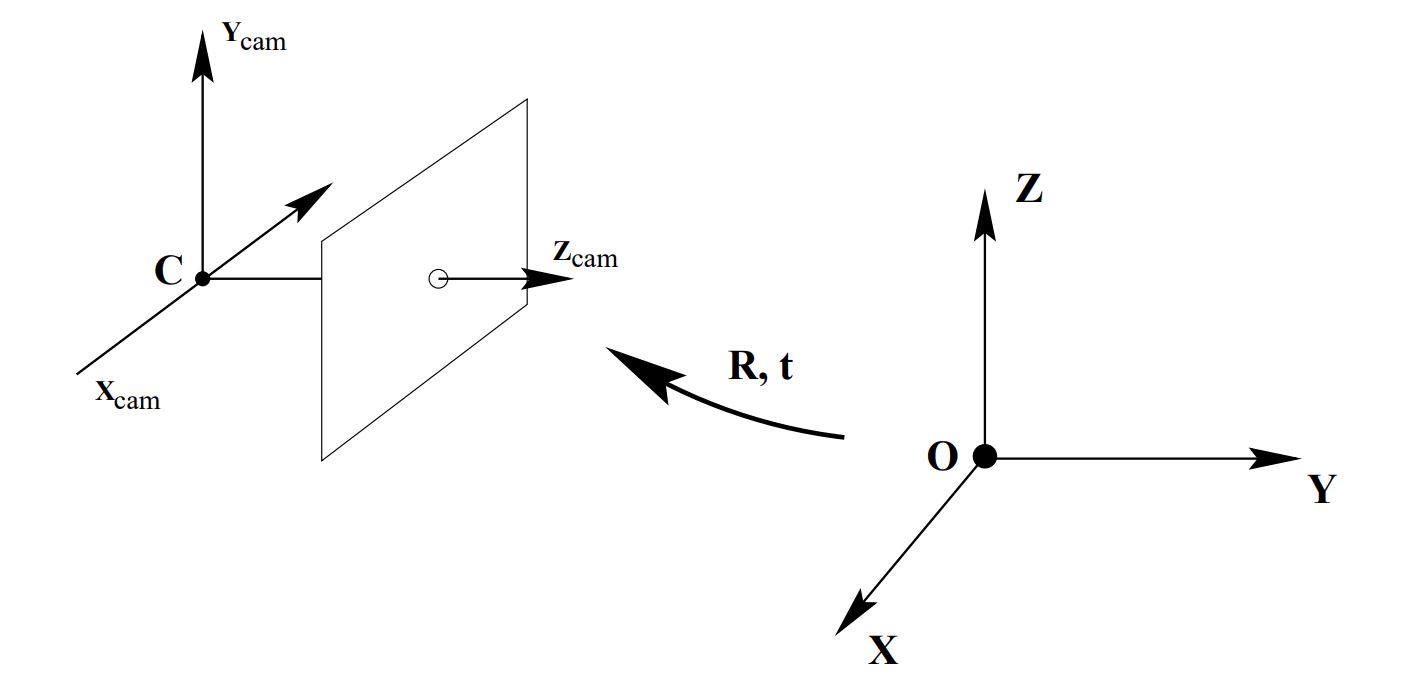
좀 더 일반적으로 camera의 centre가 Euclidean coordinate system의 origin이고 z-axis와 principal axis가 동일하다는 가정을 없애면, 위 그림에서와 같은 경우에 공간상의 점 $\tilde{\textbf{X}}$는 카메라 coordinate상의 점 $\tilde{\textbf{X}}_{cam}$으로 다음고 같이 표현할 수 있다.

 

$$ \tilde{\textbf{X}}_{cam} = R(\tilde{\textbf{X}} - \tilde{\textbf{C}}) $$

 

$$ \tilde{\textbf{X}}_{cam} = \begin{bmatrix} R & -R\tilde{\textbf{C}} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} $$

 

따라서, Euclidean space 내의 점을 다음과 같이 image plane으로 projection 하게 된다.

 

$$ \textbf{x} = KR[I | -\tilde{\textbf{C}}]\textbf{X} $$

 

수식의 간편성을 위하여 일반적으로는 camera centre를 명시적으로 표기하지 않는다. 대신 Euclidean space의 point에서 image plane으로의 projection을 직접적으로 표현한다.

 

$$ \tilde{\textbf{X}}_{cam} = R \tilde{\textbf{X}} + \textbf{t} $$

 

$$ P = K[R|\textbf{t}] \ where \ \textbf{t} = -R\tilde{\textbf{C}}$$