Target-based LiDAR-Camera Calibration

Title: Automatic Extrinsic Calibration of a Camera and a 3D LiDAR Using Line and Plane Correspondences

Authors: Lipu Zhou, Zimo Li, and Michael Kaess

*모든 그림들은 위 논문으로부터 캡처함

 

[1] Introduction

• LiDAR 와 Camera 의 extrinsic calibaration 은 두 센서 간의 상대적인 rotation 및 translation 을 추정하는 것
• 해당 논문에서는 LiDAR frame 에서 camera frame 으로의 rotation 과 translation 을 아래와 같이 표기
  • Rotation: $\textbf{R}_L^C \in SO(3)$
  • Translation: $\textbf{t}_L^C$
• 이 논문에서는 checkerboard 를 calibaration target 으로 사용하며 이 checkerboard plane 의 4 개의 boundaries 를 이용하여 두 센서 간의 relative transform 을 추정함

[2] Automatic Feature Extraction

• LiDAR 센서로 부터 관측한 point cloud 에서 4 개의 boundary lines 을 검출하고 이로 부터 checkerboard plane 의 centroid 와 각 line 의 centroid 를 추정할 수 있다.

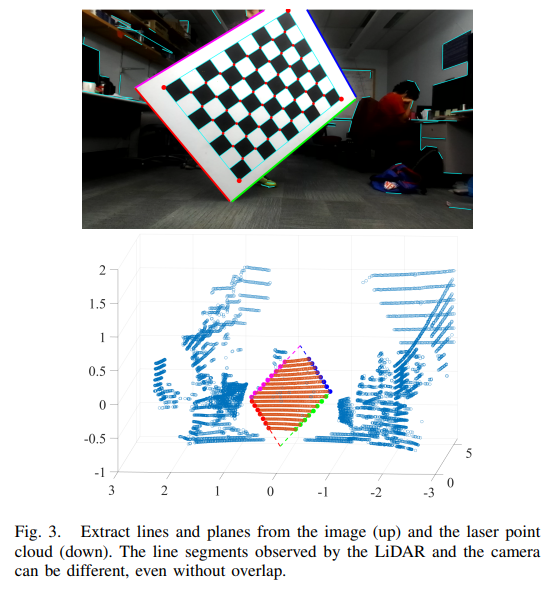
• 이 때 checkerboard point cloud 가 존재하는 공간상의 위치를 대략적으로 알고 있다고 가정하고 RANSAC plane fitting 을 통해 boundary lines 를 추정한다.

 

[3] Extrinsic Calibration

Geometric Constraints and Equivalent Set

• LiDAR frame 에서의 j 번 째 line $L_{ij}^L$ 과 camera frame 에서의 j 번째 line $L_{ij}^C$ 간의 correspondence 를 이용하여 두 센서 간 relative transform 에 관한 아래의 constraints 를 얻을 수 있다.
  • (1-a) $\textbf{R}L^C \textbf{d}{ij}^L = \textbf{d}_{ij}^C$
    • $L_{ij}^L = [\textbf{d}{ij}^L ; \textbf{p}{ij}^L]$ and $L_{ij}^C = [\textbf{d}{ij}^C ; \textbf{p}{ij}^C]$ (Direction and point vector)
  • (1-b) $(\textbf{I} - \textbf{d}{ij}^C(\textbf{d}{ij}^C)^T)(\textbf{R}L^C \textbf{Q}{ijk}^L+ \textbf{t}L^C - \textbf{P}{ij}^C ) = \textbf{0}_{3\times1}$
    • $\textbf{P}_{ij}^C$ is a point on the line in camera frame.
    • $\textbf{Q}{ijk}^L$ is a point on line $L{ij}^L$
    • $\textbf{I} - \textbf{d}{ij}^C(\textbf{d}{ij}^C)^T$ 는 projection matrix 이며 $\textbf{d}{ij}^C$ 와 평행한 직선을 $\textbf{0}{3\times1}$ 으로 보낸다.
    • $\textbf{R}L^C \textbf{Q}{ijk}^L+ \textbf{t}L^C - \textbf{P}{ij}^C$ 는 LiDAR frame 에서 j 번 째 line 위의 k 번째 point $\textbf{Q}{ijk}^L$ 를 camera frame 으로 옮기고, camera frame 에서 j 번째 line 위의 point vector $\textbf{P}{ij}^C$ 를 빼 준것으로, camera frame 에서 j 번째 line 과 평행한 line 의 direction vector 와 같다.
  • (2-a) $\textbf{R}_L^C\textbf{n}_i^L = \textbf{n}_i^C$
  • (2-b) $\textbf{n}_i^C \cdot (\textbf{R}L^C \textbf{P}{im}^L + \textbf{t}_L^C) + d_i^C = 0$
• 위 constraint 들을 만족하는 relative transform 을 최적화 방식으로 구하는 것이 해당 논문의 주된 방법론

 

• Extrinsic calibration 의 정확도를 높이기 위해서는 measurements 의 다양성을 높여야 한다. 즉 다양한 pose 의 checkerboard 를 측정할 필요가 있다.
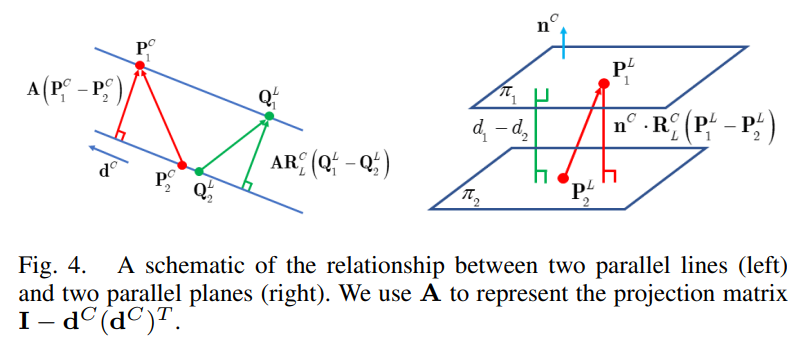
• 두 parallel 한 line 에 의해 생성되는 constraints 는 identical 하다. 예를 들어, camera frame 에서 두 parallel 한 line $L_1$ 과 $L_2$ 가 direction $\textbf{d}^C$ 로 정의된다고 가정하자. 그리고, $\textbf{I} - \textbf{d}{ij}^C(\textbf{d}{ij}^C)^T = \textbf{A}$ 라고 정의하면 (1-b) 에 의해 다음이 성립한다.
  • $\textbf{A}\textbf{t}_L^C + \textbf{A}(\textbf{R}_L^C\textbf{Q}_1^L-\textbf{P}_1^C)=0$
  • $\textbf{A}\textbf{t}_L^C + \textbf{A}(\textbf{R}_L^C\textbf{Q}_1^L-\textbf{P}_1^C)=0$
• 위 첫 번째 식의 두 번째 항을 아래와 같이 변형하면 두 번째 식의 두 번째 항과 정확히 같아진다.

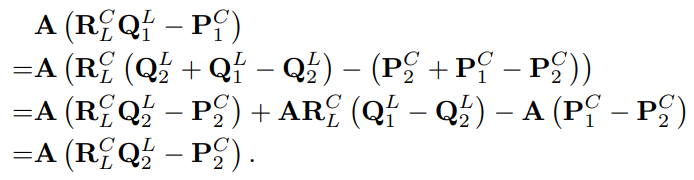
• 따라서 두 constraints 는 독립적이지 않다.
• 또한, 두 parallel 한 평면에 의해 생성되는 constraints 도 아래와 같이 같은 constraint 이다.

• 즉 위와 같은 parallel case 가 많다고 해도 이론적으로는 다양한 measurement 가 확보되었다고 할 수 없다.
• 논문에서는 checkerboard 가 가까울 수록 좋으며(더 정확한 측정이 가능하므로) 단순히 board 를 회전 시키는 것 많으로도 충분한 constraints 를 확보할 수 있다고 설명하고 있다.

 

참고 논문

[1] L. Zhou, Z. Li and M. Kaess, "Automatic Extrinsic Calibration of a Camera and a 3D LiDAR Using Line and Plane Correspondences," 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2018, pp. 5562-5569, doi: 10.1109/IROS.2018.8593660.