Robust Optimization - Huber Loss, RANSAC

이전 포스팅에서는 non-linear least squares문제에 대한 해법으로 Gradient descent, Gauss-Newton, 그리고 이 둘이 결합된 형태인 Levenberg-Marquardt 방법에 대하여 설명하였으며, 약간의 noise를 갖는 circle fitting 문제를 예제로 해당 방법들의 수렴성을 비교하였다.

https://define.tistory.com/29

Gauss-Newton Method

https://define.tistory.com/30

Levenberg-Marquardt Method

 

지난 포스팅 까지 사용한 데이터에는 noise가 포함되어 있긴 했지만, std가 0.01인 매우 작은 noise만 포함하였다. 이번 포스팅에서는 noise가 큰 데이터(outlier, 이상치)를 포함하였을 때의 최적화에 대하여 소개하고자 한다. 

1. Huber Loss

1.1 L1 and L2 error

Error를 정의하는 가장 기본적인 방식에는 L1와 L2 error 두 가지가 있다. 

$$ L_1 \ error = \frac{1}{N} \sum_i{|\hat{y}_i - y_i|} $$

$$ L_2 \ error = \frac{1}{N} \sum_i{(\hat{y}_i - y_i)^2} $$

이는 least squares 문제에서 각각 MAE(mean absolute error)와 MSE(mean square error)로 정의되며 각각 다음과 같은 특성을 가진다.

 

Error type	Value	Advantage	Disadvantage
L1	$\sum_i{|\hat{y}_i - y_i|}$	Relatively robust to outliers	Unstable around e < 1
L2	$\sum_i{(\hat{y}_i - y_i)^2}$	Stable around e<1	Relatively not robust to outliers

 

MSE의 경우 잔차의 제곱이 cost에 더해지기 때문에, 잔차가 1보다 큰 경우(대부분의 outlier가 이에 해당한다) 해당 데이터 값에 대한 오류가 크게 반영된다. 따라서 outlier 값에 과하게 bias되는 경향이 있다. L1 error는 단순 absolute value로 error를 계산하여 이를 cost에 더해주기 때문에 L2 error에 비해  outlier에 대해서는 robust하다. 반대로, 잔차가 1보다 작은 경우에는 L2 error가 해당 데이터의 오류를 더 작게 반영하기 때문에, outlier가 아닌 데이터 들에 대해서는 L2 error가 더 stable하다. 여기서 stable하다는 것은 비슷한 데이터에 대하여 모델이 얼마나 비슷하게 추정되는가에 따라 결정된다.

 

그림 1. std가 0.01인 noisy data(blue point)와 상대적으로 큰 noise를 갖고 있는 outlier data(red point)가 존재하는 상황에서의 circle fitting 결과. L1 error로 fitting한 결과(black circle)이 L2 error로 fitting한 결과(green circle)보다 상대적으로 outlier에 robust함을 확인할 수 있다.

 

위 그림과 같은 circle fitting 예제에서 std가 0.01인 noisy data(blue point)와 상대적으로 큰 noise를 갖고 있는 outlier data(red point)가 있다고 해 보자. Noise가 클 때(red point에 의한 잔차가 1보다 클 때)는 L1 error에 의한 추정 모델(black circle)이 L2 error에 의한 추정 모델(red circle) 보다 더 강건한 결과를 보인다. 하지만, 아래의 그림 2와 같이 outlier의 x좌표에 따른 모델 fitting 값을 비교해 보면 잔차가 1보다 적은 경우에는 L2 error가 더 stable한 결과를 보인다.

 

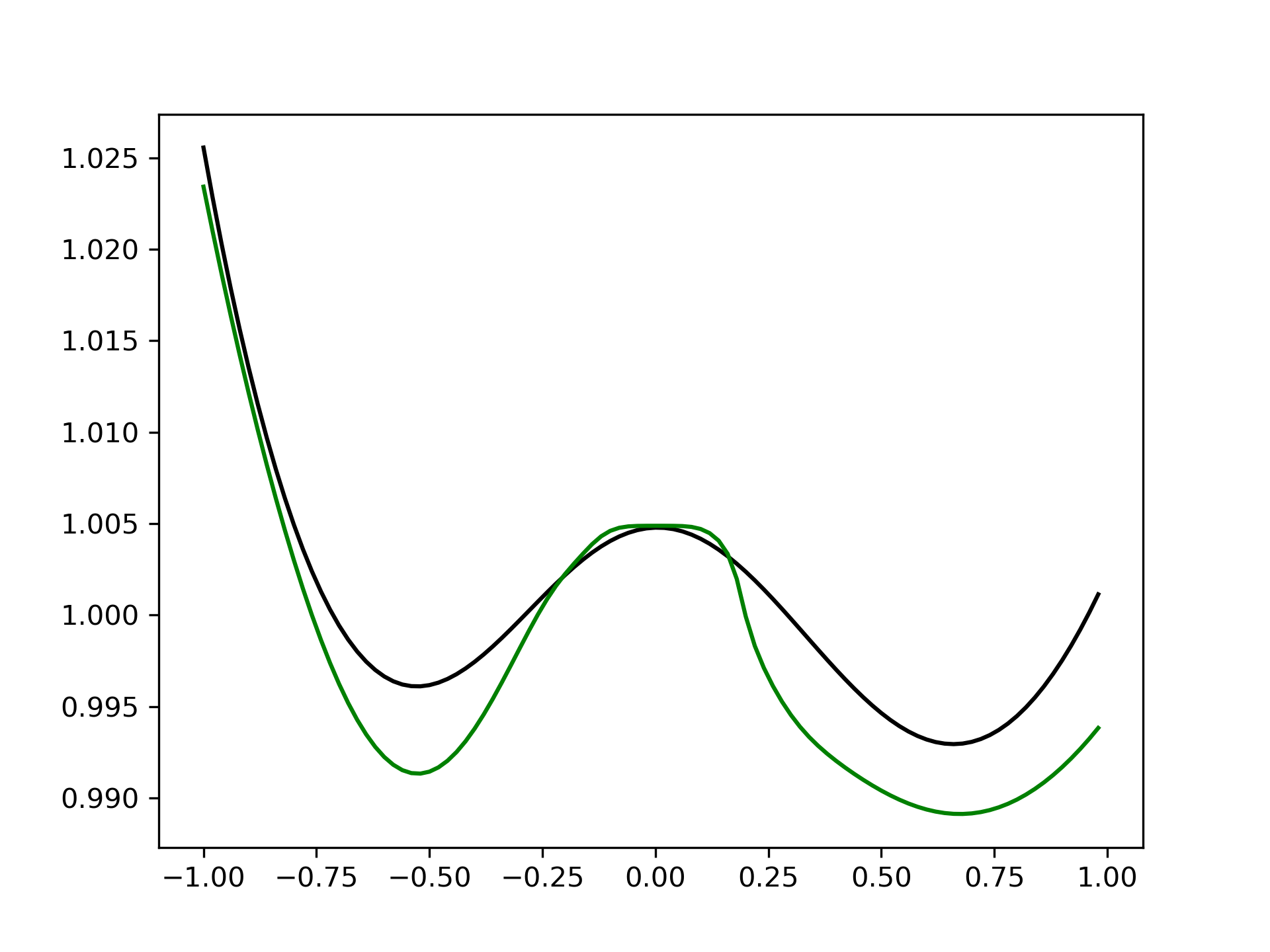
그림 2. Outlier의 x좌표에 따른 model fitting값 비교. 왼쪽부터 순서대로 모델의 a, b, r 값이다. L1 error에 의한 fitting 값은 black curve로, L2 error에 의한 fitting 값은 green curve로 표현되어 있다. 잔차가 1보다 작아지는 영역(outlier의 noise가 상대적으로 작은 영역)에서는 L2 error에 의한 fitting이 더 stable함을 확인할 수 있다.

 

1.2 Huber Loss

Huber Loss는 L1의 outlier에 대한 robustness와 L2의 inlier(outlier의 반대)에 대한 stability의 장점을 동시에 취하기 위하여 제안된 error 함수이다. 이는 다음과 같이 정의된다.

$$ L_{\delta}(e) = \begin{cases} \frac{1}{2}e^2, & \text{if} \ |e| <= \delta \\ \delta (|e|-\frac{1}{2}\delta)&\text{otherwise} \end{cases} $$

그림 3. L1, L2 그리고 huber loss의 비교

이 huber loss는 그림 3과 같이, 잔차가 $\delta$보다 작은 영역에서는 L2처럼, $\delta$보다 큰 영역에서는 L1처럼 동작한다. 또한 huber loss는 연속이고 미분가능하기 때문에 일반적인 least squares와 같이 Gradient descent, Gauss-Newton 그리고 Levenberg-Marquardt method에 적용할 수 있다.

L1, L2 그리고 Huber loss를 통한 circle fitting 비교는 그림 4에서 확인할 수 있다. 여기에서는 $\delta$값을 0.1로 설정하였다. 이 값을 크게 하면 많은 구간에서 (green line) L2와 비슷해지고 반대로 작아지면 (black line) L1과 비슷해 진다.

 

그림 4. L1, L2 그리고 Huber loss의 circle fitting 결과 비교. (red line) Huber loss를 사용한 fitting 결과가 (black line) L1과 (green line) L2의 사이에서 움직이는것을 확인할 수 있다.

 

Fitting 값 또한 그림 5와 같이 Huber loss를 이용한 fitting이 L1과 L2를 이용한 fitting 값의 가운데 있음을 확인할 수 있으며, 잔차가 클때는 L1와 가깝게(outlier의 효과를 작게), 작을때는 L2와 가깝게(stable 하게) 동작함을 확인할 수 있다.

 

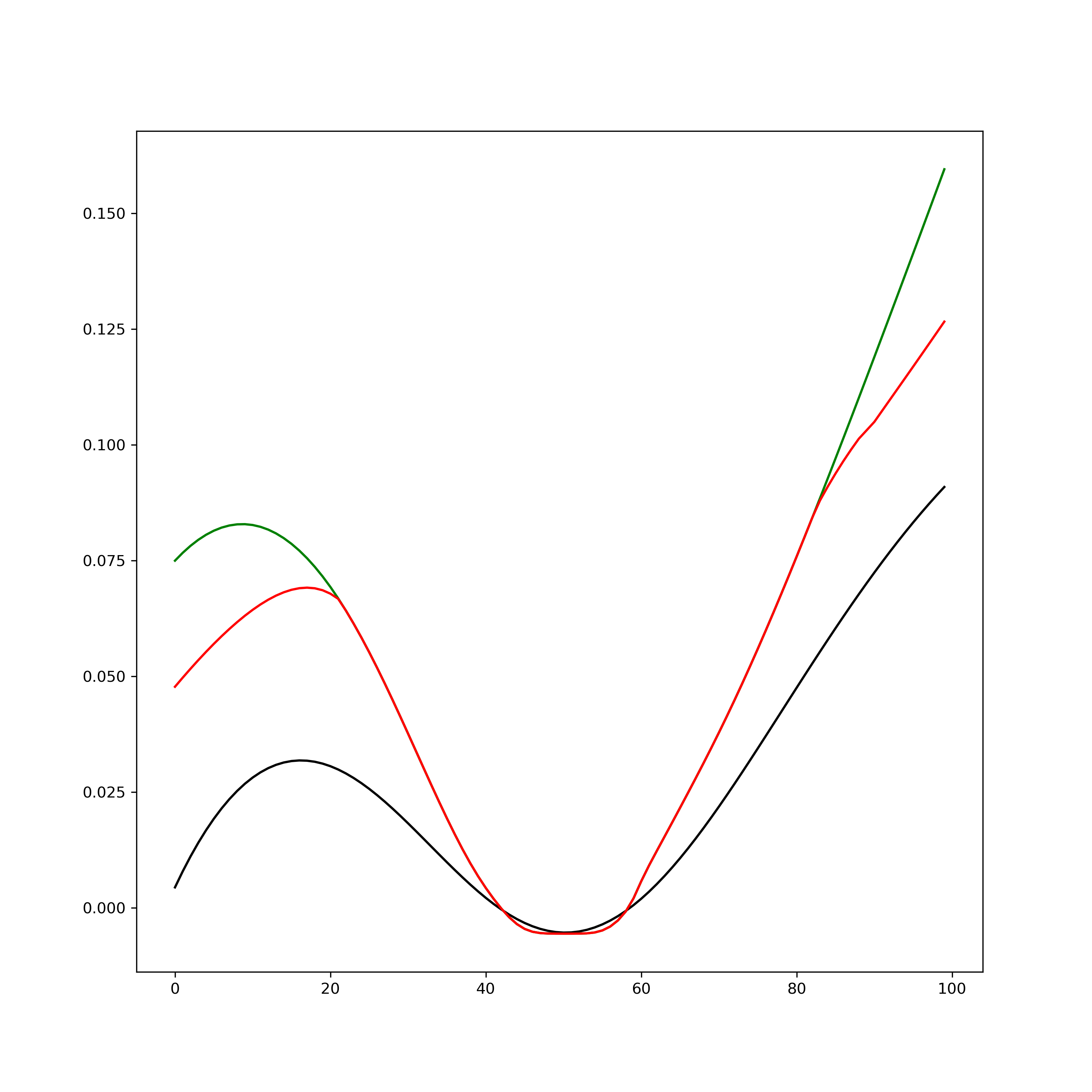
그림 5. Outlier의 x좌표에 따른 model fitting값 비교. 왼쪽부터 순서대로 모델의 a, b, r 값이다. Huber loss에 의한 fitting값이 전체적으로 L1 loss와 L2 loss에 의한 fitting값의 가운데에 있음을 확인할 수 있으며, 잔차가 클때는 L1와 가깝게(outlier의 효과를 작게), 작을때는 L2와 가깝게(stable 하게) 동작함을 확인할 수 있다.

 

Huber loss와 같은 robust least squares를 위한 loss들을 M-estimator라고 한다. 추가적인 내용은 아래의 위키를 참고하기 바란다.

https://en.wikipedia.org/wiki/M-estimator

 

 

2. RANSAC (RANdom SAmple Consensus)

 

RANSAC은 주어진 데이터에서 random하게 몇몇 샘플을 뽑아 이들을 통해 fitting하고 이 fitting결과가 전체 데이터에서 어느정도의 consensus(합의)를 갖는지 판단하여 그 중 가장 큰 consensus의 모델을 뽑는 방법이다.

RANSAC은 매우 간단하게 구현이 가능하고, outlier를 reject하는 효과가 있어 robust한 fitting을 가능하게 하지만, 결과의 random성 때문에 최악의 경우에는 전혀 다른 값으로 fitting될 수 있다는 단점이 있다.

 

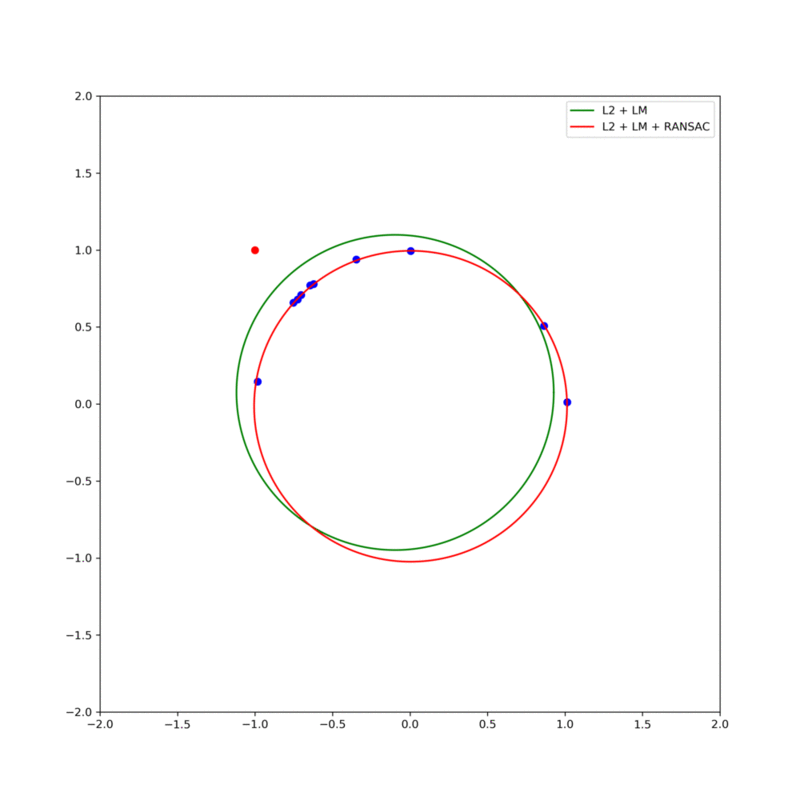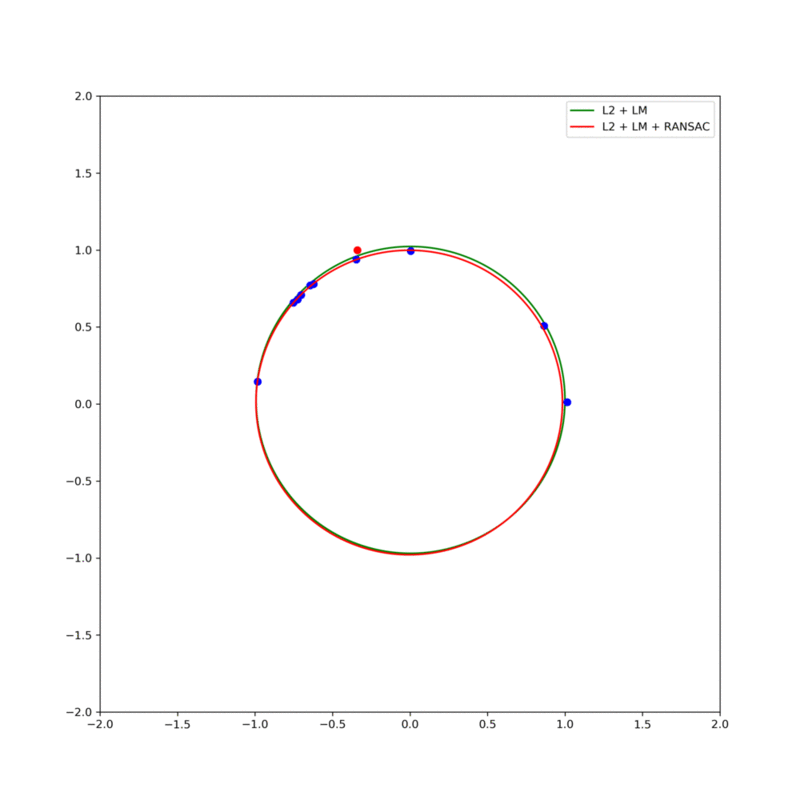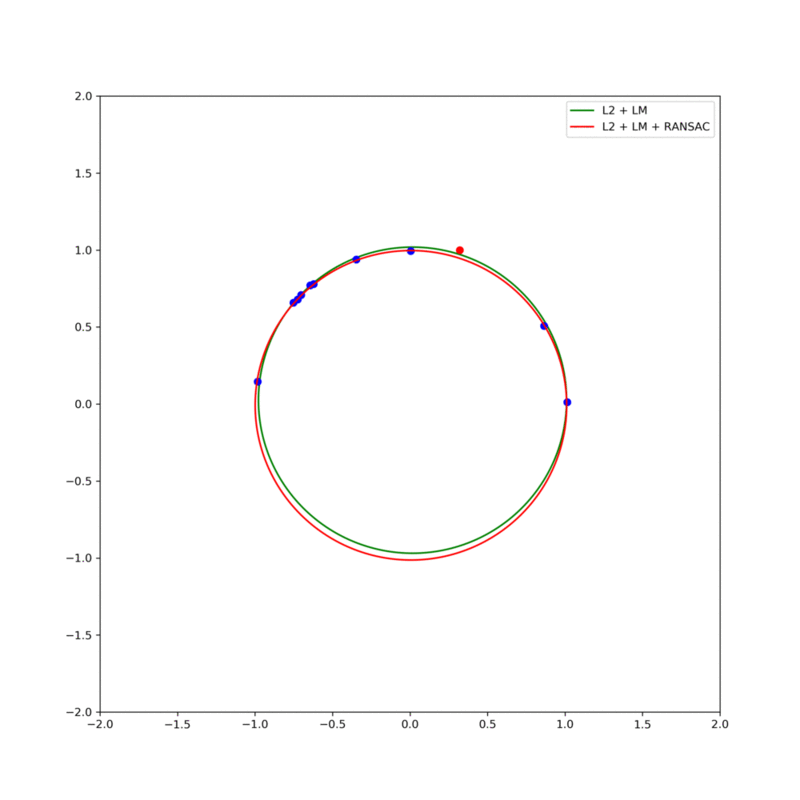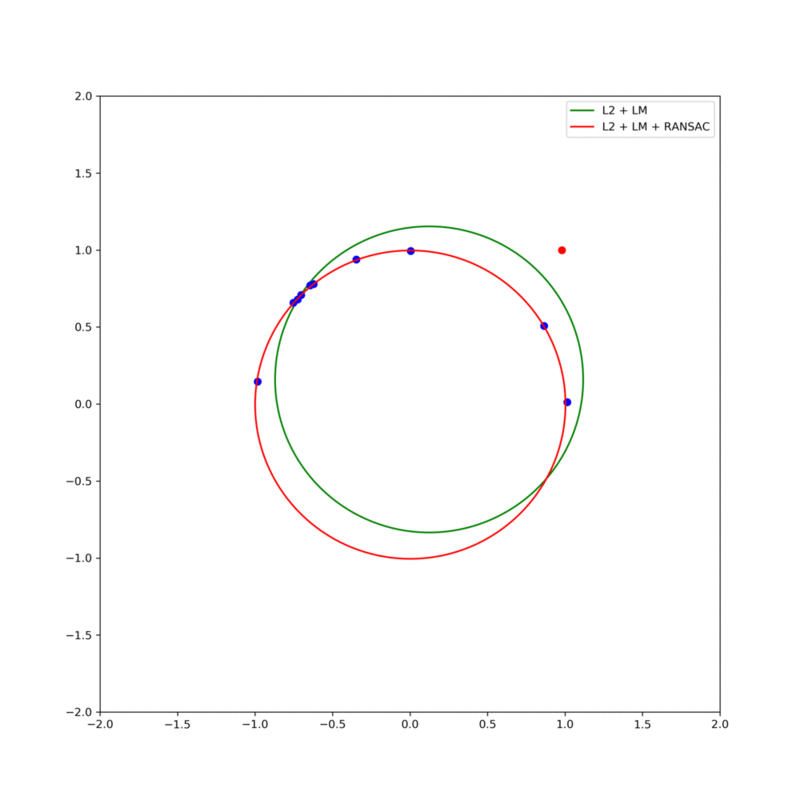
그림 6. (red line) RANSAC에 의한 fitting 결과와 (green line) 전체 데이터를 이용한 fitting 결과의 비교.

 

Consensus는 샘플을 통해 fitting된 모델에서 모든 데이터에 대한 residual을 구하고 미리 설정한 threshold값 미만의 residual을 가진 데이터는 해당 모델에 '합의'한 것으로 간주된다. 따라서, 합의한 데이터의 개수가 가장 많은 모델은 best fit 모델로 정한다.