Levenberg-Marquardt Method

1. Introduction

앞선 자료들에서 대표적인 함수 최적화 방법으로 gradient descent와 Gauss-Newton method에 대하여 소개한 바 있다. Gradient descent는 선형 함수에서만 간단히 소개하였으나, 비선형 함수에서도 그 기본 원리는 같다. 자세한 내용은 아래를 참고하길 바란다.

 

Gradient Descent : https://define.tistory.com/28

Linear Regression

Gauss-Newton : https://define.tistory.com/29

Non-linear Least Squares Method

 

Gauss-Newton method의 핵심은 비선형(non-linear)함수를 지역적으로 선형함수로 근사하여 해를 구하는 데 있다. 즉, 현재 매개변수(parameter) 추정값 근처에서 오차 함수 또는 목적 함수를 선형화 하여 최소 제곱 해를 구하고 구해진 해 근처에서 같은 과정을 반복하는 것 이다.

 

Levenberg-Marquardt (LM) method는 Gauss-Newton과 gradient descent가 결합된 형태로서 현재 매개변수 값이 해로부터 멀리 떨어져 있을때 gradient descent방식으로 동작하고 해 근처에서는 Gauss-Newton 방식으로 동작한다. LM method는 Gauss-Newton method 보다 빠르고 안정적인 수렴을 보여주기 때문에 비선형 최적화 문제에서는 일반적으로 이것이 사용된다.

 

2. Levenberg-Marquardt Method

 

Gradient descent 방법은 gradient의 반대방향으로 매개변수를 이동하는 방법으로 이동 크기는 gradient의 크기에 비례한다. Gauss-Newton 방법은 지역적인 gradient를 구한다는것 까지는 gradient descent와 같으나 gradient와 curvature(곡률)을 같이 고려하면서 해를 찾는다. 두 방법의 식은 아래와 같다.

 

$$ Gradient \ Descent \ : \ \textbf{x}_{k+1} = \textbf{x}_k - \alpha J^TF $$

 

$$ Gauss-Newton \ : \ \textbf{x}_{k+1} = \textbf{x}_k - (J^TJ)^{-1}J^TF $$

 

이 때, $J^TJ$가 2차 미분인 Hessian의 근사 행렬이므로, Gauss-Newton이 1차 미분을 통한 근사에서 출발하였으나 결론적으로 2차 미분을 통한 근사와 같이 동작한다는 것을 알 수 있다.

 

Gauss-Newton는 이동할 step의 크기를 (gradient/curvature)로 결정하는데, 이는 gradient의 변화가 급격하면(curvature가 크면) 조금만 이동하고, gradient의 변화가 적으면(curvature가 작으면) 좀 더 크게 이동함으로써 해를 찾아 나가는 방식이다. Gauss-Newton이  gradient descent보다 더 정확하고 빠르게 해를 찾을 수 있다는 것이 알려져 있으나, $J^TJ$가 singular 에 가까울 경우 수치적으로 불안정하여 해가 발산할 수 있는 문제점이 있다.

 

Levenberg Method는 이 두 방법을 혼합한 것이며 다음과 같은 식으로 표현된다.

 

$$\textbf{x}_{k+1} = \textbf{x}_k - (J^TJ + \mu* I)^{-1} J^TF $$

 

즉, Gauss-Newton 방식에 gradient descent 방식을 혼합함으로써 수치적 불안정으로 부터 야기되는 해의 발산에 대한 위험성을 낮추고자 하였다. $\mu$는 damping factor라고 부르는데 이 값이 낮으면 Gauss-Newton과 유사해지고, 반대의 경우에는 gradient descent와 유사해지는데, gradient descent와 유사하게 동작할 경우 수렴 속도가 느리다는 문제가 있다.

 

Levenberg-Marquardt method는 Levenberg method가 gradient descent 방식으로 동작할 때 수렴 속도가 느리다는 단점을 보완하기 위하여 고안되었다. 수식은 아래와 같다.

 

$$\textbf{x}_{k+1} = \textbf{x}_k - (J^TJ + \mu*  diag(J^TJ))^{-1} J^TF $$

 

즉, 항등 행렬($I$) 대신 $diag(J^TJ)$를 곱해주는 것 인데, $J^TJ$가 Hessian의 근사행렬임을 생각해 볼 때, $J^TJ$의 대각 원소들은 각 매개변수 축으로의 곡률을 의미한다. Gauss-Newton이 곡률을 반영함으로써 gradient descent에 비해 해를 더 빠르고 안정적으로 해를 찾는다는것을 생각해볼 때, gradient descent에 역시 곡률을 반영하여 이러한 이점을 취하고자 함임을 알 수 있다.

 

3. Circle Fitting

 

여기에서는 기존에 다루었던 circle fitting 문제를 통해 Gaussian-Newton 방식과 gradient descent 그리고 Levenberg-Marquardt method의 수렴성을 비교한다.

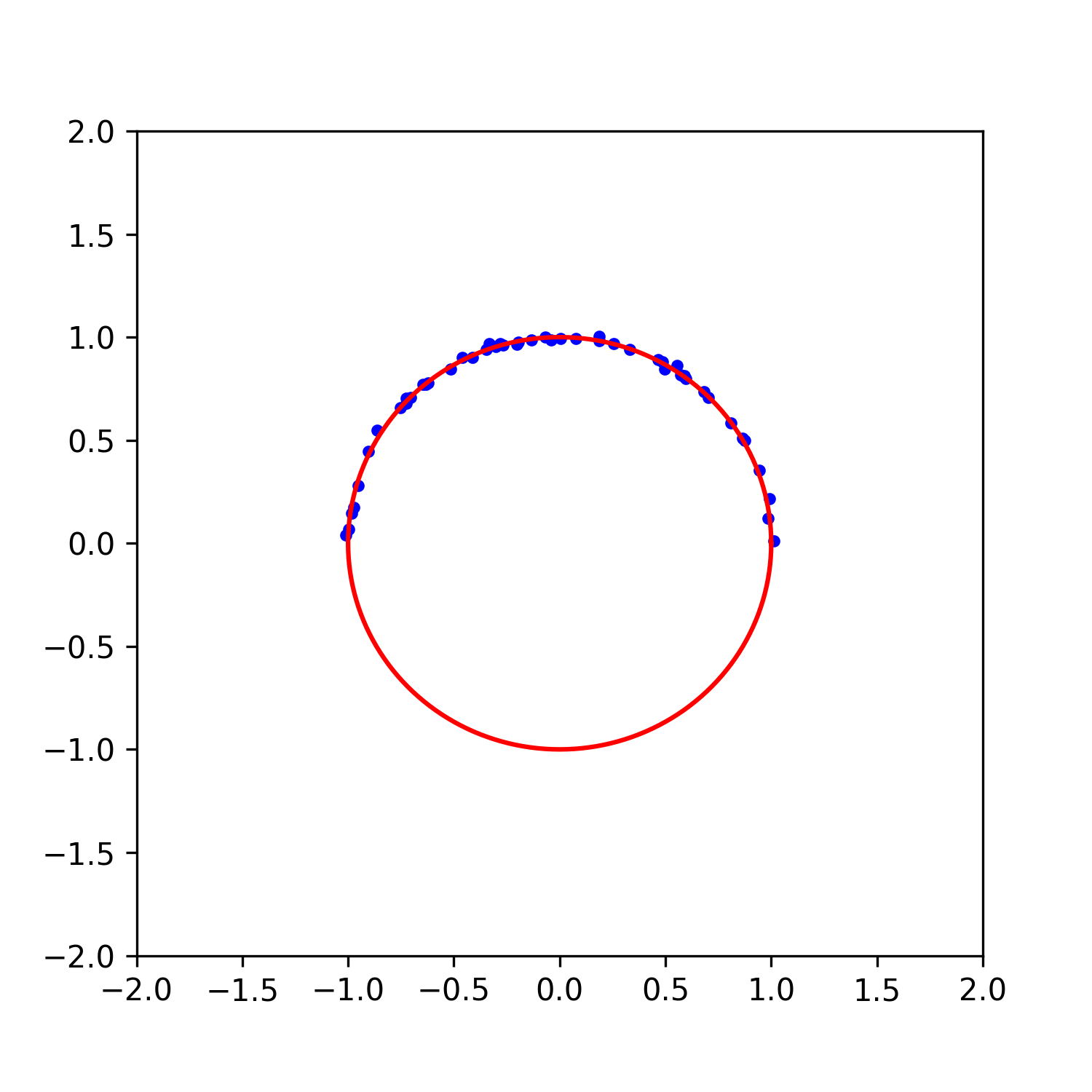
그림 1. 중심이 (0, 0)이고 반지름이 1인 원(red line)으로 부터 sampling된 반원 데이터(blue points). 평균이 0이고 표준편차가 $\sigma=0.01$인 noise를 포함한다.

 

Circle fitting 문제는 위 그림 1과 같이 중심이 (0, 0)이고 반지름의 길이가 1인 원(red line)으로 부터 sampling된 반원 데이터(blue points)에 가장 잘 맞는 원을 구하는 문제로 자세한 문제의 내용은 아래의 글을 참고하기 바란다.

 

https://define.tistory.com/29

Non-linear Least Squares Method

 

Circle fitting 문제는 다음과 같이 정의된다.

 

$$ model : \sqrt{(x_i-a)^2+(y_i-b)^2} = r $$

$$ optimal circle = [a^*, \ b^*, \ r^*] $$

$$ a^*, b^*, r^* =  \underset{a,b,r}{argmin} \sum_i^N{\Big{(} \sqrt{(x_i-a)^2+(y_i-b)^2} -r \Big{)}^2} $$

 

따라서 F와 J를 다음과 같이 정의할 수 있다.

$$ F = \begin{bmatrix} \Big{(}  \sqrt{(x_1-a)^2+(y_1-b)^2} -r \Big{)}^2 \\ \vdots \\ \Big{(} \sqrt{(x_n-a)^2+(y_n-b)^2} - r \Big{)}^2  \end{bmatrix} = \begin{bmatrix} F_1 \\ \vdots \\ F_n \end{bmatrix} $$

 

$$ J = \begin{bmatrix} \frac{\partial{F_1}}{\partial{a}} \ \frac{\partial{F_1}}{\partial{b}} \ \frac{\partial{F_1}}{\partial{r}} \\ \vdots \\ \frac{\partial{F_n}}{\partial{a}} \ \frac{\partial{F_n}}{\partial{b}} \ \frac{\partial{F_n}}{\partial{r}} \end{bmatrix} $$ 

 

$$ J =2 \begin{bmatrix} \sqrt{(x_1-a)^2+(y_1-b)^2} - r \\ \vdots \\ \sqrt{(x_n-a)^2+(y_n-b)^2} - r \end{bmatrix}   \bigodot \begin{bmatrix} \frac{a-x_1}{\sqrt{(x_1-a)^2+(y_1-b)^2}} \ \frac{b-y_1}{\sqrt{(x_1-a)^2+(y_1-b)^2}} \ -1 \\ \vdots \\ \frac{a-x_n}{\sqrt{(x_n-a)^2+(y_n-b)^2}} \ \frac{b-y_n}{\sqrt{(x_n-a)^2+(y_n-b)^2}} \ -1  \end{bmatrix} $$

 

이렇게 구한 Jabobiand과 F로 gradient descent, Gauss-Newton, Levenberg-Marquardt 방식을 사용하여 circle fitting을 한 결과는 다음의 그림과 같다.

 

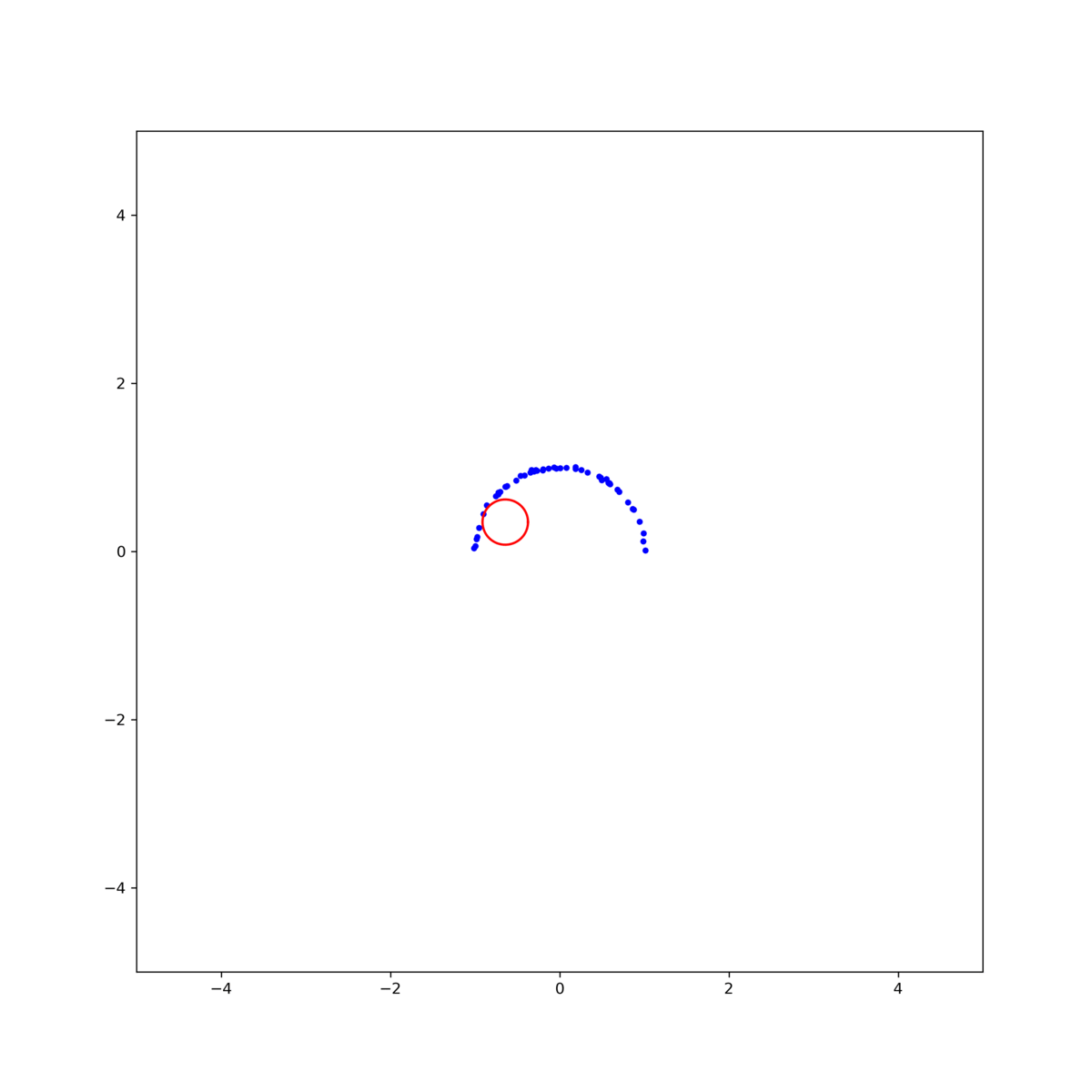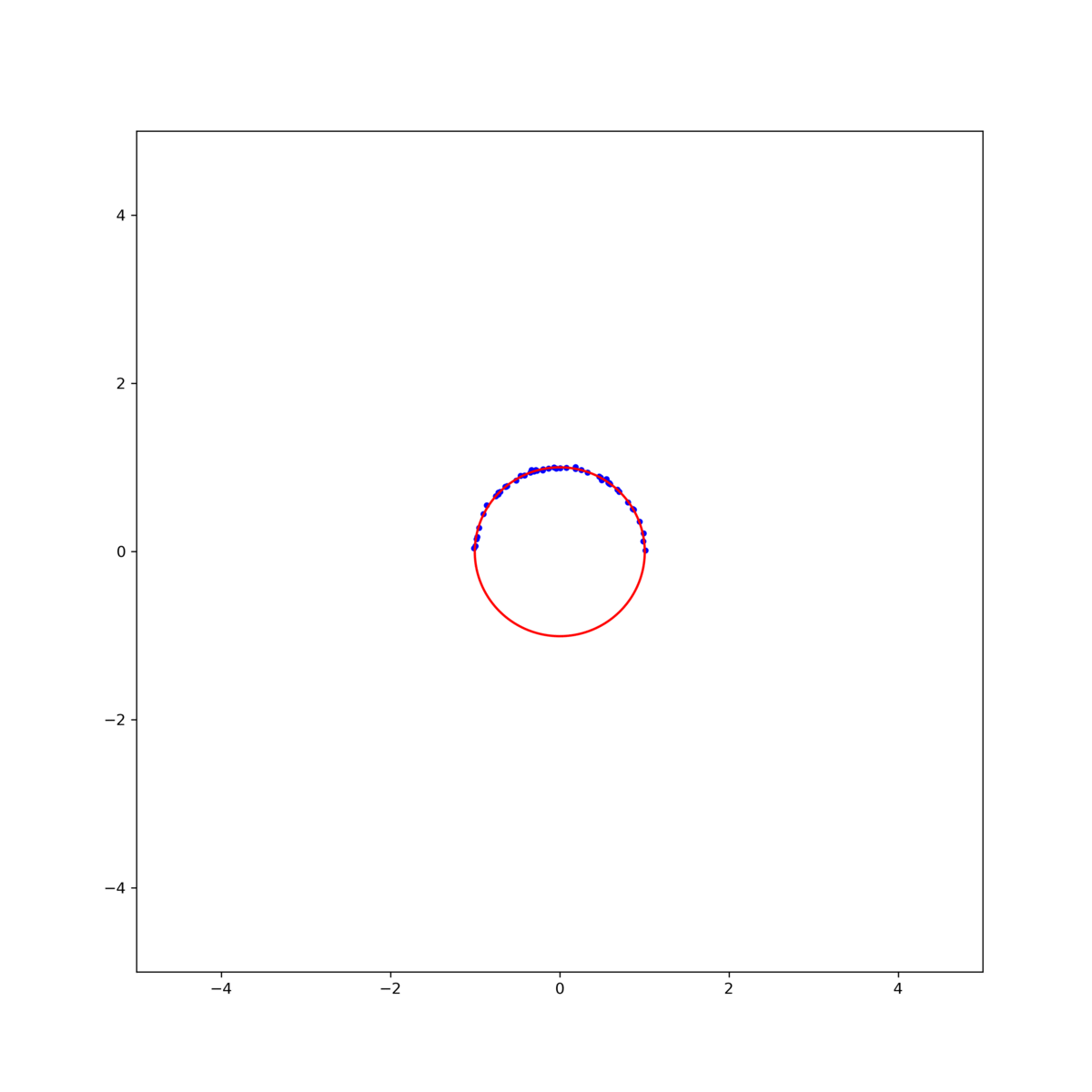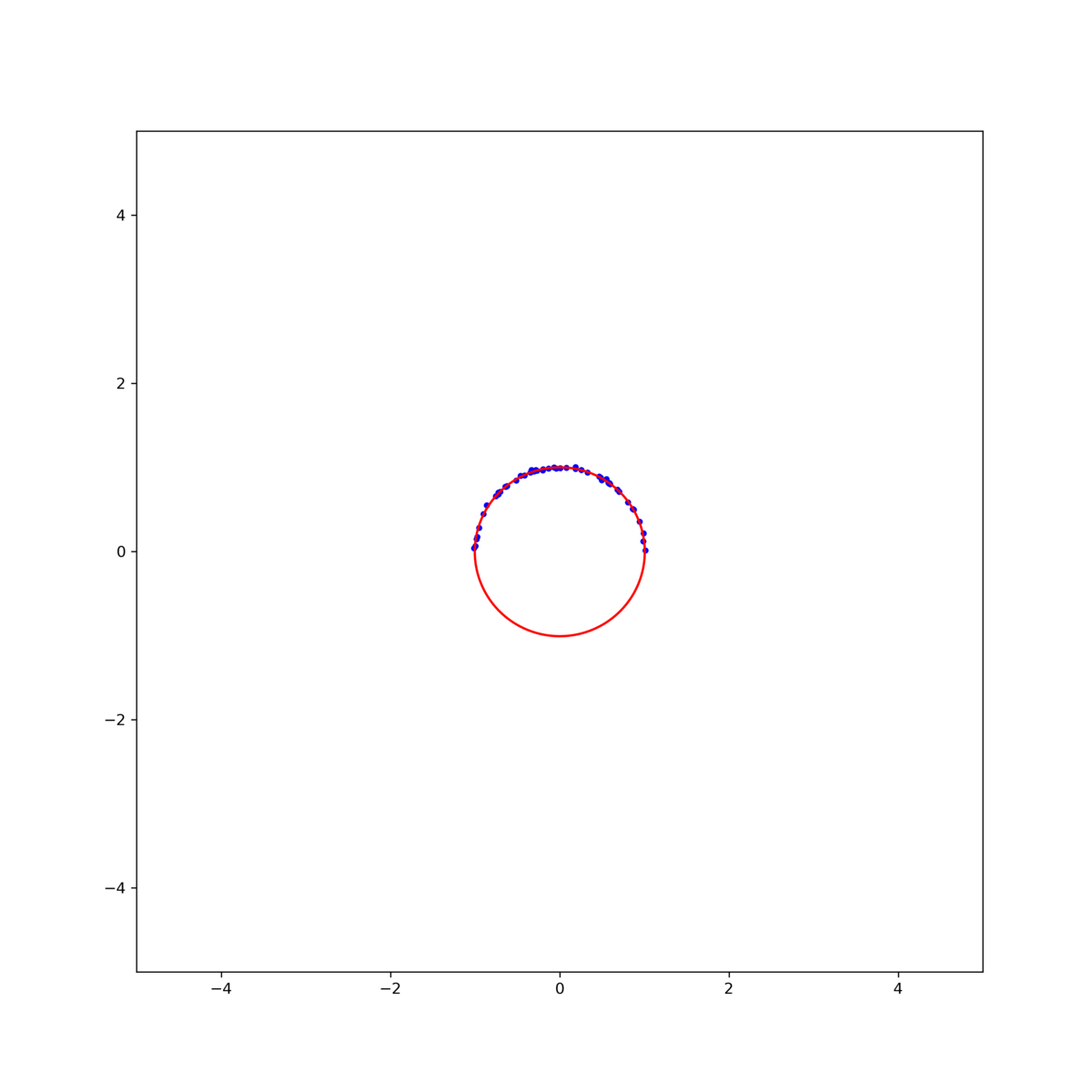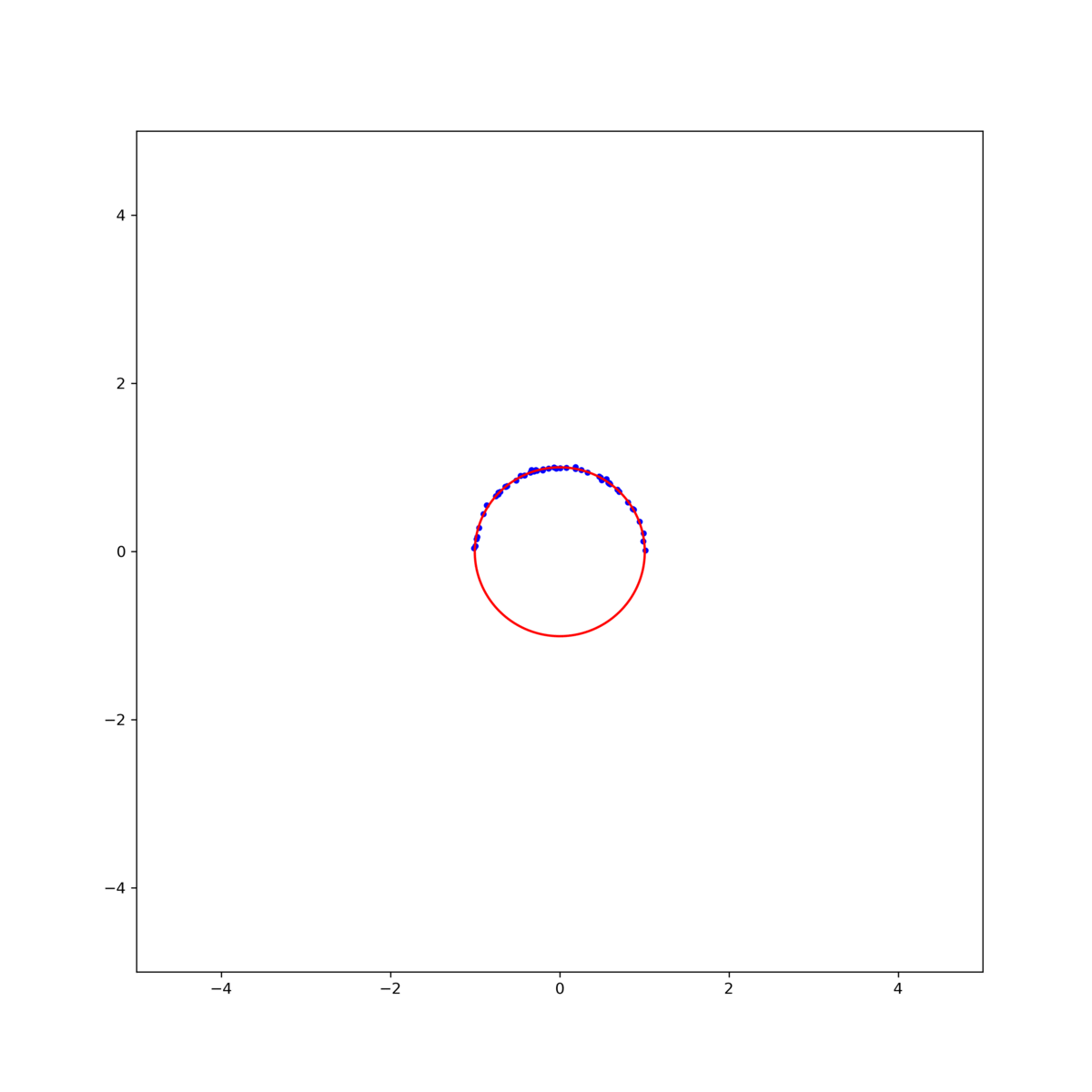
그림 2. (left)Gradient descent, (middle)Gauss-Newton, (right)Levenberg-Marquardt 방식을 이용한 circle fitting의 비교. $\textbf{x}_0$ = [0.8, -0.5, 1]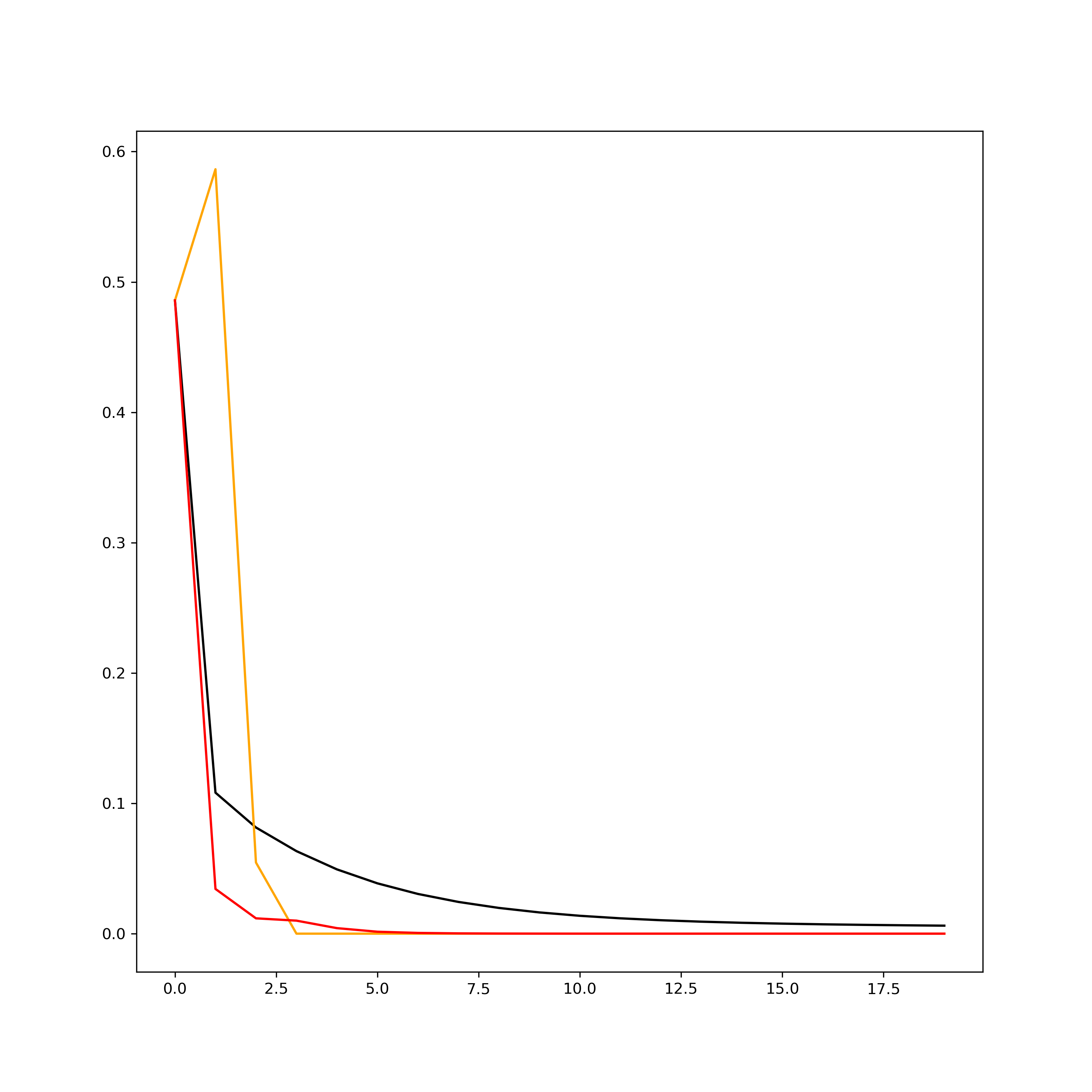

그림 3. 각 method의 iteration에 따른 MSE. (black line)Gradient descent, (orange line)Gauss-Newton, (red line)Levenberg-Marquardt

 

결과를 보면, Gauss-Newton이 가장 빨리 수렴하지만 Levenberg-Marquardt 방식이 더 안정적으로 해에 접근하는것을 확인할 수 있다. 이는 초기값을 바꾸어 해를 구해보면 더 명확히 확인할 수 있다. 그림 2의 결과에서 초기값을 $\textbf{x}_0$ = [1, -0.5, 1] 로 조금만 바꾸어도 Gauss-Newton은 발산하지만 Levenberg-Marquardt는 해에 수렴함을 확인할 수 있다 (그림 4).

 

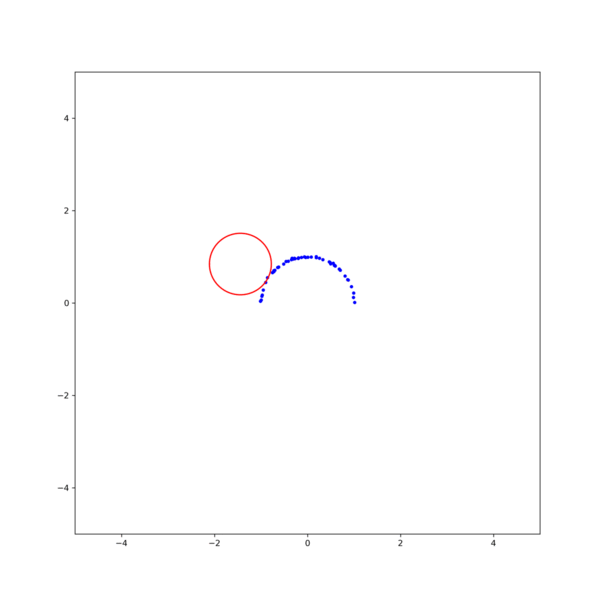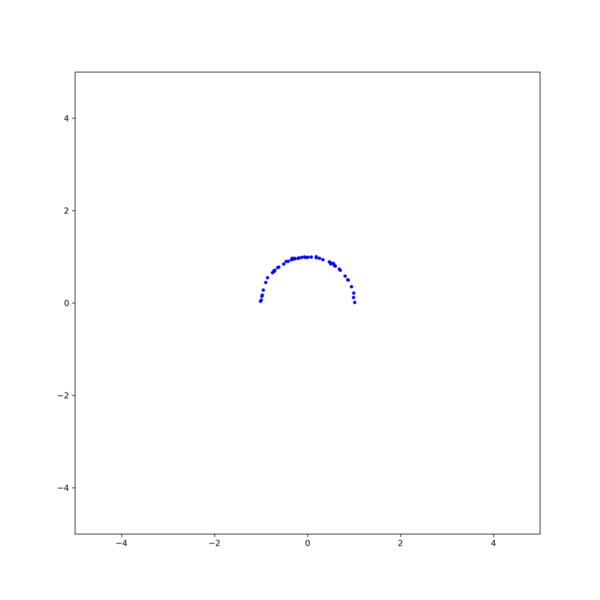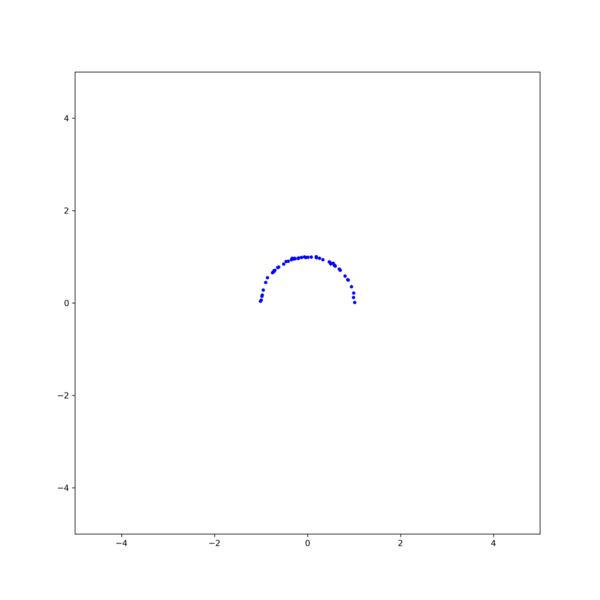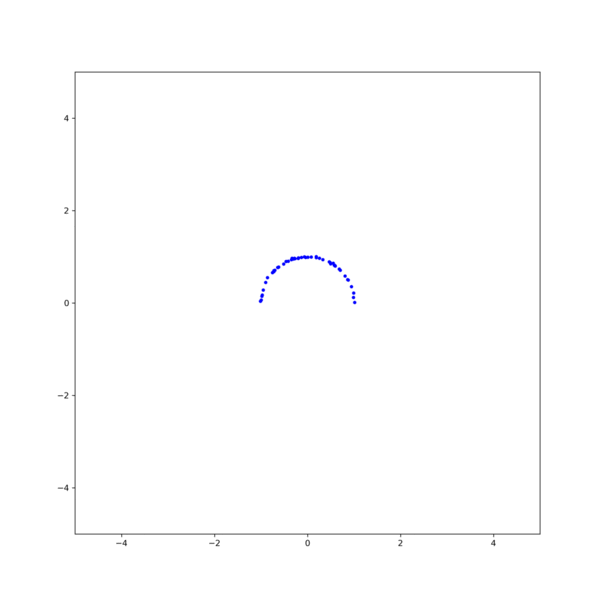
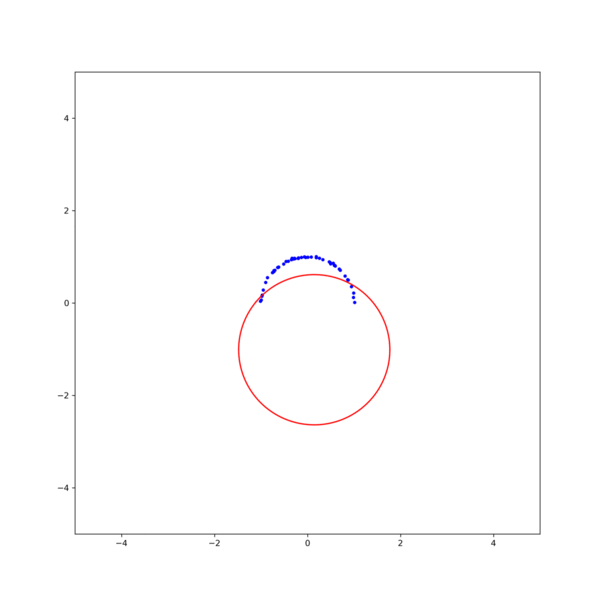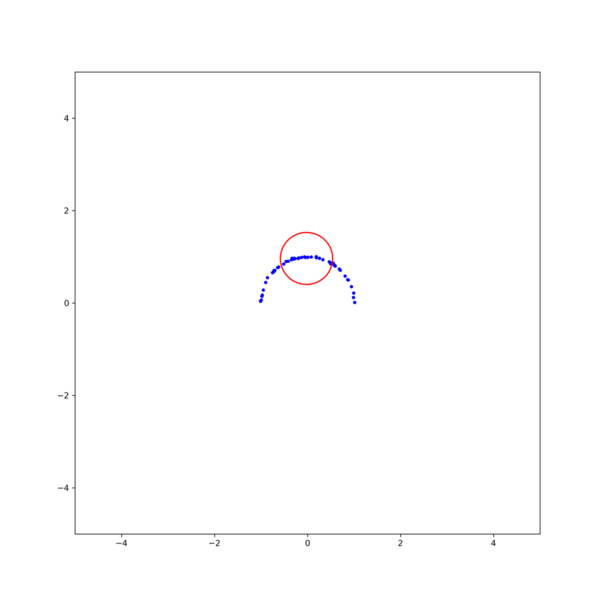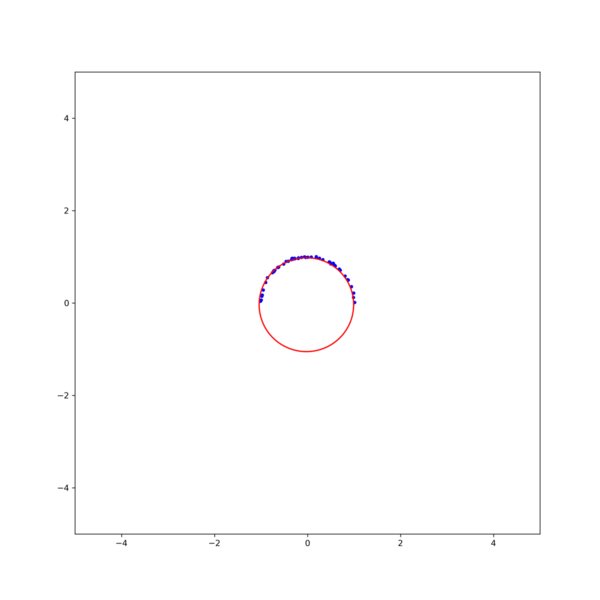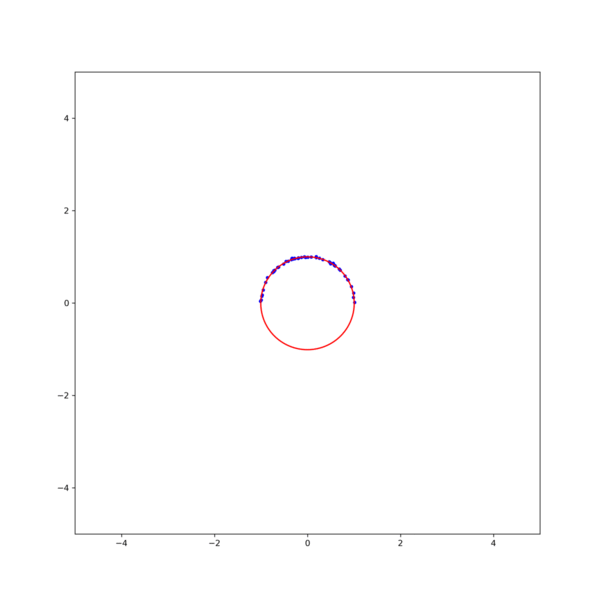
그림 4. (left)Gauss-Newton, (right)Levenberg-Marquardt 방식을 이용한 circle fitting의 비교. $\textbf{x}_0$ = [1, -0.5, 1]

 

 

[1] Gavin, H.. “The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems.” (2013).