(ICP)Iterative Closest Point

github: https://github.com/93won/2D_LiDAR_Odom_ICP

 

1. Iterative Closest Point

Iterative closest point는 서로 다른 두 개의 점군(point cloud)을 정합(registration)시키는 대표적인 알고리즘 중 하나로 LiDAR 센서를 이용한 센서 pose 추정(pose estimation, localization)에 주로 이용된다. 여기에서는 해당 응용 예에 대하여 설명한다.

예를 들어, 그림 1의 왼쪽 그림과 같이 서로 다른 두 시점에서 2D LiDAR 센서로부터 두 점군이 얻어졌다고 해 보자. 먼저 관측된 점군을 transform (translaton + rotation)하였을 때 이후 관측된 점군과 잘 정합된다면 이 것이 두 시간 사이의 센서의 상대적 transform 이라고 추정할 수 있다.

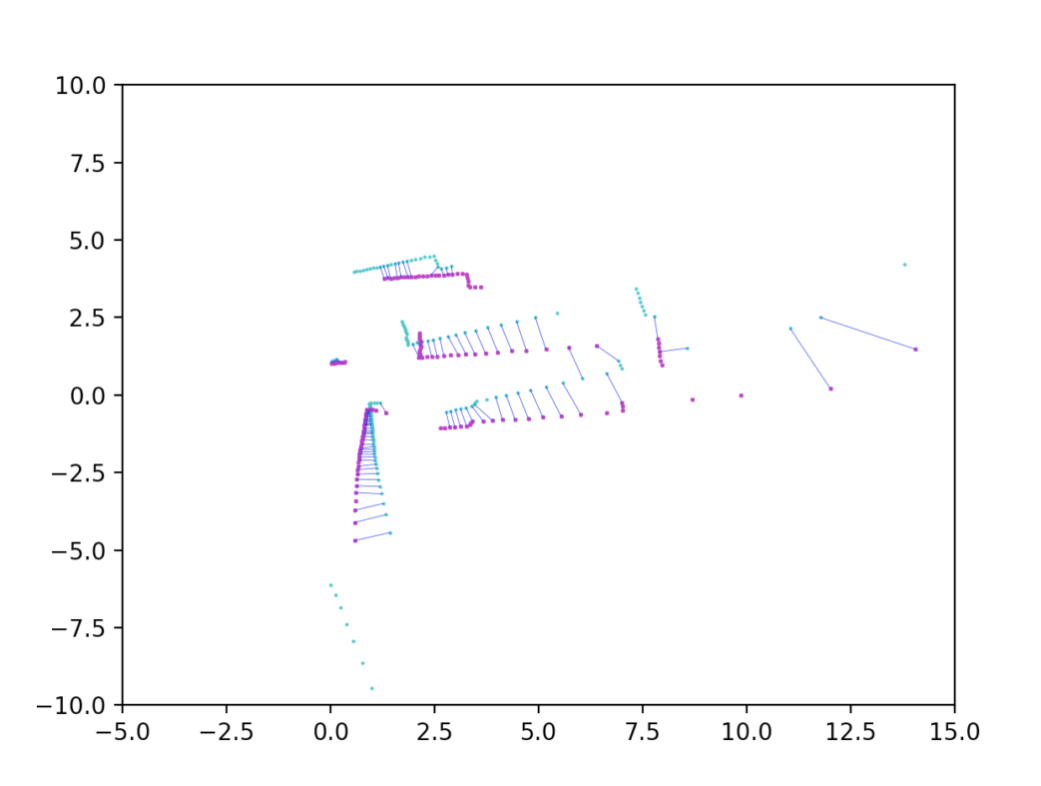
그림 1. (left) 서로 다른 시간에서 측정된 두 센서 데이터. (right) closest neighbors

두 점군 간의 상대적 transform을 구하기 위한 단계는 아래와 같다.

(1) 두 점군의 point들 간의 matching을 결정한다(closest neighbors) - 그림 1의 오른쪽

(2) 정합 오차(registration error)를 최소화 하는 transform을 구하여 이전에 관측된 데이터를 transform한다.

두 단계를 수행하면 아래의 그림 2와 같이 정합된 결과를 얻을 수 있으며 이 과정을 오차가 수렴할 때 까지 반복한다.

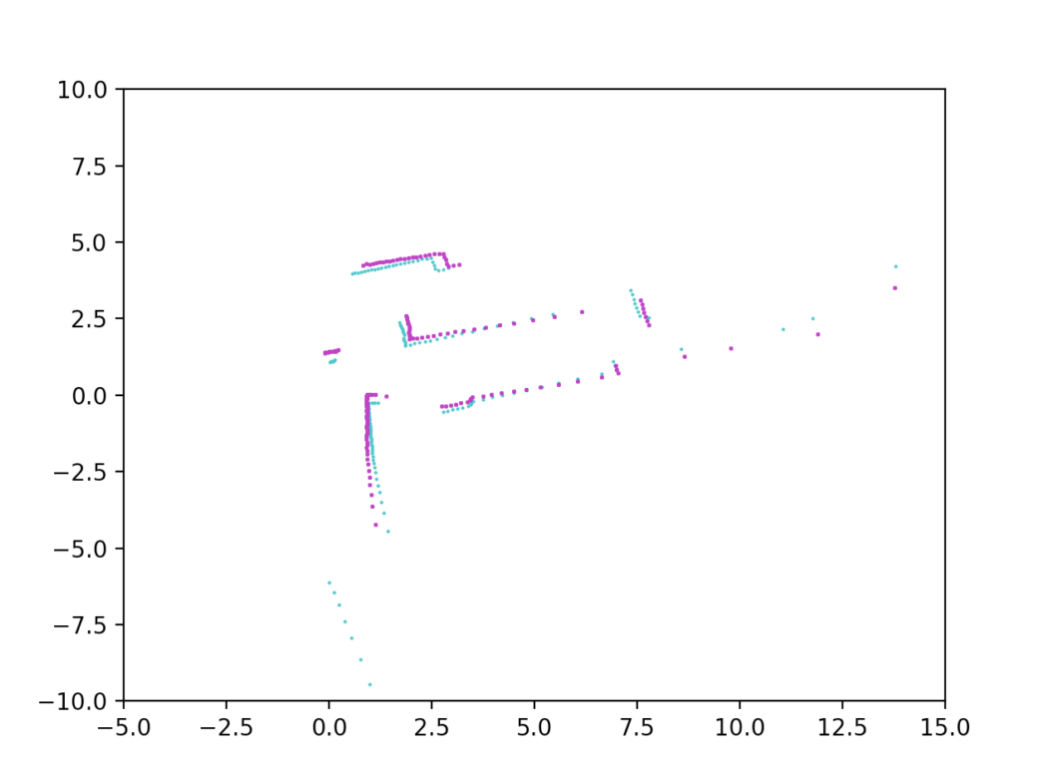
그림 2. 두 점군간의 registration

 

2. Least Squares

정합 오차를 최소화 하는 것은 일종의 Least Squares 문제이다. 시각 t-1과 t에서 관측된 i번째 데이터 쌍을 각각 $\textbf{x}_{t-1, i} = [x_{t-1,i}, \  y_{t-1,i}]^T$와 $\textbf{x}_{t,i} = [x_{t,i}, \  y_{t,i}]^T$라고 하면, 다음과 같이 문제를 정의할 수 있다.

$$T^* = \underset{T}{argmin} \frac{1}{N} \sum_i^N{||T\textbf{s}_{t-1, i} - \textbf{s}_{t,i}||^2}$$

$$ \textbf{s} = [x \ y \ 1]^T $$

$$ T=\begin{bmatrix} cos\theta \ -sin\theta \ t_x \\ sin\theta \ \ \ \ cos\theta \ \ t_y \\ 0 \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ 1 \end{bmatrix} $$

위 문제를 풀기 위해, 먼저 가장 적절한 회전 변환R을 찾는다. 이를 위해 아래의 식과 같이 구해진 두 scan 데이터 집합에 각각 해당 scan 데이터의 평균을 빼 주어, 평행이동 시킨다.

$$ \textbf{x}_{t-1, i}' = [x_{t-1,i} - \mu_{t-1,i, x} , \  y_{t-1,i} - \mu_{t-1,i, y}]^T$$

$$ \textbf{x}_{t, i}' = [x_{t,i} - \mu_{t,i, x} , \  y_{t,i} - \mu_{t,i, y}]^T$$

그런 다음, 아래의 식을 최소화하는 변환 R을 구한다.

$$ R^* = \underset{R}{argmin} \frac{1}{N} \sum_i^N{(R\textbf{x}_{t-1, i}' - \textbf{x}_{t,i}')^2}$$

위 식을 최소화 하는 변환 R을 구하기 위해 식을 전개하면, 다음과 같다.

$$ \frac{1}{N} \sum_i^N{||R\textbf{x}_{t-1, i}' - \textbf{x}_{t,i}'||^2} = -\frac{1}{N} \sum_i^N{2\textbf{x}_{t,i}'^TR\textbf{x}_{t-1, i}' + const.}   $$

따라서 이 문제는 다시 다음과 같이 정의할 수 있다.

$$ R^* = \underset{R}{argmax} \sum_i^N{\textbf{x}_{t,i}'^TR\textbf{x}_{t-1, i}'} = \sum_i^N{Trace(R\textbf{x}_{t-1, i}'\textbf{x}_{t,i}'^T)}$$

이 때, $X=\begin{bmatrix} \textbf{x}_1 \\ \vdots \\ \textbf{x}_N \end{bmatrix}$,  $H = \textbf{X}_{t-1}'\textbf{X}_{t}'^T$로 두면 $R^* = \underset{R}{argmax} Trace(RH)$ 이다.

이 $H$를 Singular value decomposition(SVD) 하면, $H=UDV^T$를 얻는데, 여기서 singular value는 모두 0 이상이기 때문에 $RH=VU^T UDV^T = VDV^T$는 positive semidefinite이고, 따라서 임의의 orthonormal 변환 $B$에 대해서 2.1의 Lemma를 만족하므로 $R^*$는 $VU^T$임을 알 수 있다.

따라서 ICP에서 두 scan간의 회전을 $VU^T$로 계산하며 translation은 간단하게 두 평균간의 거리로 결정한다. 

2.1 Lemma

임의의 positive semidefinite matrix $AA^T$  와 임의의 orthonormal matrix $B$에 대해서 다음 식이 성립한다.

$$ Trace(AA^T) >= Trace(BAA^T) $$

이는 다음과 같이 증명 가능하다.